TECHNOLOGY BEHIND
Chemical Compounds DEEP PROFILING SERVICES
For Any Chemical Compound comprising C, H, N, O, S, F, Cl, Br, I, Si, P, and/or As.
- Outline
- Chemical Space Generation
- Molecular Descriptor Estimation
- Quantum Chemical Computation
- Statistical Thermodynamics
- QSPR Modeling
- Neural Network Modeling
- Reliability Validation
- Patents
Outline
This page provides a summary of the development of our QSQN technology. Below is an overview of the QSQN components, which integrates Quantum Chemistry, Statistical Thermodynamics, QSPR (Quantitative Structure–Property Relationships), and Neural Networks:
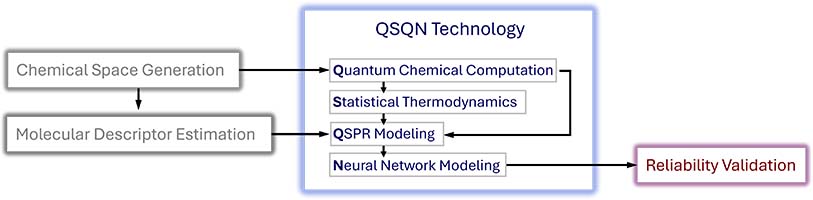
3D structures of chemical compounds are generated using a chemical space generation program. Molecular descriptor estimation and quantum chemical computations are conducted on these 3D structures. Statistical thermodynamics is then applied, utilizing the results obtained from the quantum computations. The information obtained from molecular descriptor estimation, quantum computations, and statistical thermodynamics applications is fed into the QSPR modeling. The results of the QSPR modeling are refined by applying the Neural Network model. The QSQN technology produces a comprehensive set of thermo-physicochemical, thermodynamic, transport, and pharmaceutical properties, all of which have undergone a systematic reliability validation.
Chemical Space Generation
The 3D structures of chemical compounds are generated using our chemical space generation program developed in house. The structure generation engine automatically generates all the possible structures based on the formula ranges (type of atoms & the ranges of their numbers) input by the user. For instance, if C22H46 is entered, a total of 2,278,658 structures are generated in minutes. The program automatically outputs the InChI, SMILES string, IUPAC names, and 3D structure (MOL) data.
Molecular Descriptor Estimation
Using the generated 3D structures, molecular descriptors are estimated based on their definition described by Todeschini and Consonni. Over 2,000 descriptors are produced for each compound, organized into 24 distinct categories detailed in our full information list. High-quality 3D descriptors, such as molecular orbital energies and electrostatic descriptors, necessitate the results from quantum chemical computations. Reliable sets of these molecular descriptors are also produced based on the results obtained from the quantum chemical computations described below.
Quantum Chemical Computation
As the reliability of geometry optimization heavily relies on the initial structure, our quantum chemical computation process begins with securing a “good” initial structure through a detailed conformer analysis. Multiple conformers are automatically generated, and potential energy calculations for each conformer are performed based on the MMFF94s force field proposed by Halgren. Depending on the number of single bonds, up to hundreds of conformers can be generated. The conformer with the lowest potential energy is selected as the initial structure.
A systematic investigation, including over 2,000 trial computations, has been conducted to determine an optimal combination of computational methods (e.g., Hartree-Fock, Density Functional Theory) and basis sets (e.g., STO-3G, 6-31G*). This was to ensure a reliable prediction of thermo-physicochemical, thermodynamic, transport, and pharmaceutical properties. Based on the accuracy analysis of predicting entropies, dipole moments, frequencies, heat capacities, magnetic susceptibilities, polarizabilities, radii of gyration, van der Waals areas, and volumes, an optimal combination was concluded. For compounds containing C, H, N, O, and S, the DFT-B3LYP functional with the 6-31G* basis set followed by RI-MP2 energy correction with the cc-pVDZ basis set was found to provide decent accuracy and reasonable computation time. For compounds containing atoms other than C, H, N, O, and S, the B3LYP method with the 3-21G* basis set without energy correction was determined as the optimal choice.
Geometry optimization and frequency calculation are performed with an emphasis on hindered rotor corrections, an important step for a reliable prediction of the various properties. The optimized structures are carefully verified to ensure the absence of imaginary frequencies. Analytical calculations are also carried out to obtain detailed spectra data.
Statistical Thermodynamics
Empirical formulas lacking a scientific principles or parameters without physical meaning often lead to unreliable predictions when applied beyond experimental ranges. Statistical thermodynamics has been applied as a basis of mechanistic modeling, rooted in proven scientific principles, to enhance the prediction reliability. For instance, a mathematical expression of heat capacity of ideal gas is given by:
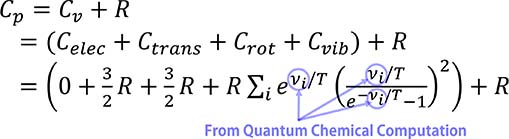
The vibrational contributions are determined by the values of vibrational frequencies (vi) obtained from the quantum chemical frequency calculations, which include hindered rotor corrections crucial for reliable prediction.
While quantum chemical information and statistical thermodynamics typically yield reliable models, they are not infallible. Instances where these models underperform have been addressed by incorporating QSPR and neural network models, which are explained in further detail in the following sections. Not all properties can be described by statistical thermodynamics alone; in such cases, QSPR and neural network methodologies were utilized to fill in the gaps where mathematical expressions from statistical thermodynamics are unavailable.
QSPR Modeling
QSPR modeling has been performed using the refined experimental data detailed on our Reliability webpage and the statistical thermodynamics results if applicable. The selection of independent variables involved over 2,000 descriptors across 24 distinct categories.
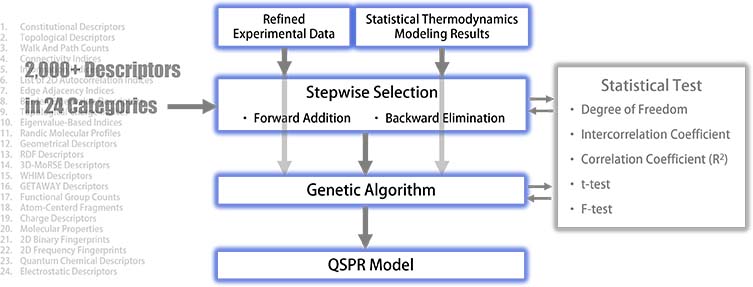
The initial phase of modeling employed stepwise approaches —both forward selection and backward elimination—to identify the necessary descriptors achieving an acceptable squared correlation coefficient (R²) and passing the F-test for statistical significance. The number of chemical compounds, for which refined experimental data were available for each property, fell within the orders of 1,000 to 10,000 in most cases. This breadth of data ensured a statistically significant degree of freedom, thanks to the large-scale, collected and refined experimental datasets detailed on our Reliability webpage. The intercorrelation coefficients among descriptors were meticulously scrutinized to ensure an adequate level of independence. The parameter estimates from the multilinear regression were considered meaningful only when their t-values are statistically significant.
Once the stepwise selection was successful, descriptor information was input into a genetic algorithm as hyperparameters to search the entire descriptor space for optimum descriptor combinations. Metrics such as the intercorrelation coefficient, t-value, squared correlation coefficient (R²), and F-value were carefully checked during the genetic algorithm phase. When all criteria were satisfied, the QSPR modeling process was completed.
High-quality 3D descriptors obtained from the quantum chemical computations were found to play a crucial role in developing a reliable QSPR model.
Neural Network Modeling
QSPR modeling assumes a linear relationship between the property and its descriptors, which does not account for the nonlinear nature of their relationship. To address this limitation, neural network modeling has been employed, enhancing the ability to capture the nonlinearity. In this model, the input layer nodes correspond to the descriptors used in the QSPR model, while a single node in the output layer represents the property being predicted.
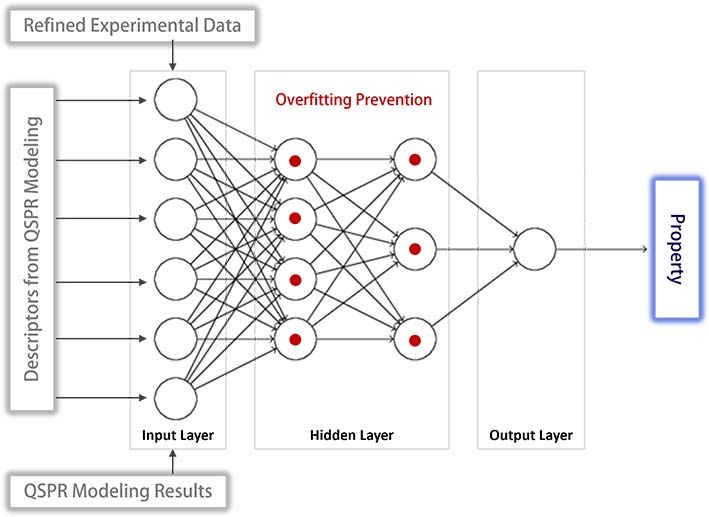
Special attention has been given to mitigating the common issue of overfitting in neural network modeling. The detection of overfitting is based on cross-validation, utilizing both refined experimental datasets and the results from QSPR modeling. Upon identifying overfitting, preventative measures are implemented. These include reducing the number of hidden layers, decreasing the number of nodes within these layers, and adjusting specific node weights.
Extensive experimentation has indicated that optimal performance is generally achieved when the neural network consists of a single hidden layer. Furthermore, the number of nodes in this hidden layer should typically be fewer than those in the input layer to effectively prevent overfitting. The refined neural network models have demonstrated an improvement, with increases in the squared correlation coefficient (R²) values by up to approximately 7%, compared to the results from QSPR models.
Reliability Validation
The thermo-physicochemical, thermodynamic, transport, and pharmaceutical properties produced by the QSQN approach have been rigorously validated using over 1.5 million experimental data points. These data were collected over a period of 5 years from more than 160,000 diverse sources, including journal articles, scientific books, patents, and chemical databases. The QSQN approach has demonstrated an average prediction accuracy of over 95%. Its output has been extensively utilized by more than 1 million researchers worldwide and has received citations in prestigious scientific publications, such as NATURE, ELSEVIER, and journals from the American Chemical Society. Detailed information about this validation process and its outcomes is available on the Reliability webpage.
Patents
The QSQN technology has been registered under 41 Korean patents, which is listed below:
| NO. | Title | Reg. No. |
|---|---|---|
| 1 | Multiple Linear Regression-Artificial Neural Network Model Predicting Ideal Gas Absolute Entropy of Pure Organic Compound for Normal State | 10-1267376 |
| 2 | Multiple Linear Regression-Artificial Neural Network Hybrid Model Predicting Acentric Factor of Pure Organic Compound | 10-1325101 |
| 3 | Multiple Linear Regression-Artificial Neural Network Hybrid Model Predicting Critical Pressure of Pure Organic Compound | 10-1325103 |
| 4 | Multiple Linear Regression-Artificial Neural Network Hybrid Model Predicting Critical Temperature of Pure Organic Compound | 10-1325107 |
| 5 | Multiple Linear Regression-Artificial Neural Network Hybrid Model Predicting Critical Volume of Pure Organic Compound | 10-1325125 |
| 6 | Multiple Linear Regression-Artificial Neural Network Hybrid Model Predicting Energesis of Ideal Gas of Pure Organic Compound | 10-1325097 |
| 7 | Multiple Linear Regression-Artificial Neural Network Hybrid Model Predicting Enthalpy of Fusion at Melting Point of Pure Organic Compound | 10-1325112 |
| 8 | Multiple Linear Regression-Artificial Neural Network Hybrid Model Predicting Saturated Liquid Density of Pure rganic Compound at 298.15K | 10-1325120 |
| 9 | Multiple Linear Regression-Artificial Neural Network Hybrid Model Predicting Normal Boiling Point of Pure Organic Compound | 10-1313026 |
| 10 | Multiple Linear Regression-Artificial Neural Network Hybrid Model Predicting Refractive Index of Pure Organic Compound | 10-1313021 |
| 11 | Multiple Linear Regression-Artificial Neural Network Hybrid Model Predicting Solubility Index of Organic Compound | 10-1267391 |
| 12 | Multiple Linear Regression-Artificial Neural Network Hybrid Model Predicting Standard State Absolute Entropy of Pure Organic Compound | 10-1267356 |
| 13 | Multiple Linear Regression-Artificial Neural Network Model Predicting Standard State Enthalpy of Formation of Pure Organic Compound | 10-1267373 |
| 14 | Multiple Linear Regression-Artificial Neural Network Hybrid Model Predicting Magnetic Susceptibility of Pure Organic Compound | 10-1289322 |
| 15 | Multiple Linear Regression-Artificial Neural Network Model Predicting Polarizability of Pure Organic Compound | 10-1300633 |
| 16 | Multiple Linear Regression-Artificial Neural Network Hybrid Model Predicting Ionizing Energy of Pure Organic Compound | 10-1267381 |
| 17 | Multiple Linear Regression Model Predicting Electron Affinity of Pure Organic Compound | 10-1289323 |
| 18 | Multiple Linear Regression-Artificial Neural Network Hybrid Model Predicting Parachor of Pure Organic Compound | 10-1297211 |
| 19 | Multiple Linear Regression-Artificial Neural Network Model Predicting Flash Point of Pure Organic Compound | 10-1300628 |
| 20 | Multiple Linear Regression- Artificial Neural Network Hybrid Model Predicting Lower Flammability Limit Temperature of Pure Organic Compound | 10-1267418 |
| 21 | Multiple Linear Regression-Artificial Neural Network Hybrid Model Predicting Lower Flammability Limit Volume Percent of Organic Compound | 10-1295861 |
| 22 | Multiple Linear Regression-Artificial Neural Network Hybrid Model Predicting Upper Flammability Limit Temperature of Organic Compound | 10-1313037 |
| 23 | Multiple Linear Regression-Artificial Neural Network Hybrid Model Predicting Upper Flammability Limit Volume Percent of Pure Organic Compound | 10-1300629 |
| 24 | Multiple Linear Regression-Artificial Neural Network Hybrid Model Predicting Liquid Density of Pure Organic Compound for Normal Boiling Point | 10-1267408 |
| 25 | Multiple Linear Regression-Artificial Neural Network Hybrid Model Predicting Heat of Vaporization of Pure Organic Compound for 298K | 10-1313030 |
| 26 | Multiple Linear Regression-Artificial Neural Network Hybrid Model Predicting Heat of Vaporization of Pure Organic Compound at Normal Boiling Point | 10-1313031 |
| 27 | Multiple Linear Regression-Artificial Neural Network Hybrid Model Predicting Octanol-Water Partition Coefficient of Pure Organic Compound | 10-1295865 |
| 28 | Multiple Linear Regression-Artificial Neural Network Hybrid Model Predicting Water Solubility of Pure Organic Compound | 10-1267372 |
| 29 | Multiple Linear Regression-Artificial Neural Network Hybrid Model Predicting Heat Capacity of Ideal Gas of Organic Compound | 10-1258859 |
| 30 | SVRC Model Predicting Heat Capacity of Liquid of Pure Organic Compound | 10-1325117 |
| 31 | SVRC Model Predicting Evaporation Heat of Pure Organic Compound | 10-1267385 |
| 32 | SVRC Model Predicting Saturated Liquid Density of Pure Organic Compound | 10-1267386 |
| 33 | QSPR Model Predicting Surface Tension of Liquid of Pure Organic Compound | 10-1325124 |
| 34 | SVRC Model Predicting Thermal Conductivity of Liquid of Pure Organic Compound | 10-1302460 |
| 35 | SVRC Model Predicting Thermal Conductivity of Gas of Pure Organic Compound | 10-1295859 |
| 36 | SVRC Model Predicting Vapor Pressure of Liquid of Pure Organic Compound | 10-1258863 |
| 37 | SVRC Model Predicting Liquid Viscosity of Pure Organic Compound | 10-1313035 |
| 38 | SVRC Model Predicting Gas Viscosity of Pure Organic Compound | 10-1313036 |
| 39 | Mathematical Model Predicting Second Virial Coefficient of Pure Organic Compound Through Boyle Temperature Prediction | 10-1267369 |
| 40 | Automatic Method Using Quantum Mechanics Calculation Program and Materials Property Predictive Module and System therefor | 10-1262045 |
| 41 | Method for Predicting a Property of Compound and System for Predicting a Property of Compound | 10-1375672 |